小5算数「帯グラフと円グラフ」指導アイデア《複数のグラフから情報を読み取る》

執筆/福岡県太宰府市立水城西小学校指導教諭・寺戸和心
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元の展開
第1時 単元の導入
▼
第2時 帯グラフや円グラフの仕組みを理解し、データの特徴を読み取る。
▼
第3時 帯グラフや円グラフのかき方を理解する。
▼
第4時(本時)複数のグラフから情報を適切に読み取り、データの特徴を読み取る。
▼
第5時 帯グラフや円グラフを使った統計的な問題解決の方法について知り、身の回りの統計的事象の問題解決に生かす。
▼
第6時 学習の内容の理解を確認する。
本時のねらい
表、棒グラフ、帯グラフを関連付けながら情報を適切に読み取り、データの特徴を読み取ることができる。(思考・判断・表現)
評価規準
表から基準量、帯グラフから割合を読み取り、それらを関連付けて比較量を求めることによって、判断の根拠を説明することができる。
本時の展開
※まず、次の帯グラフを提示する。
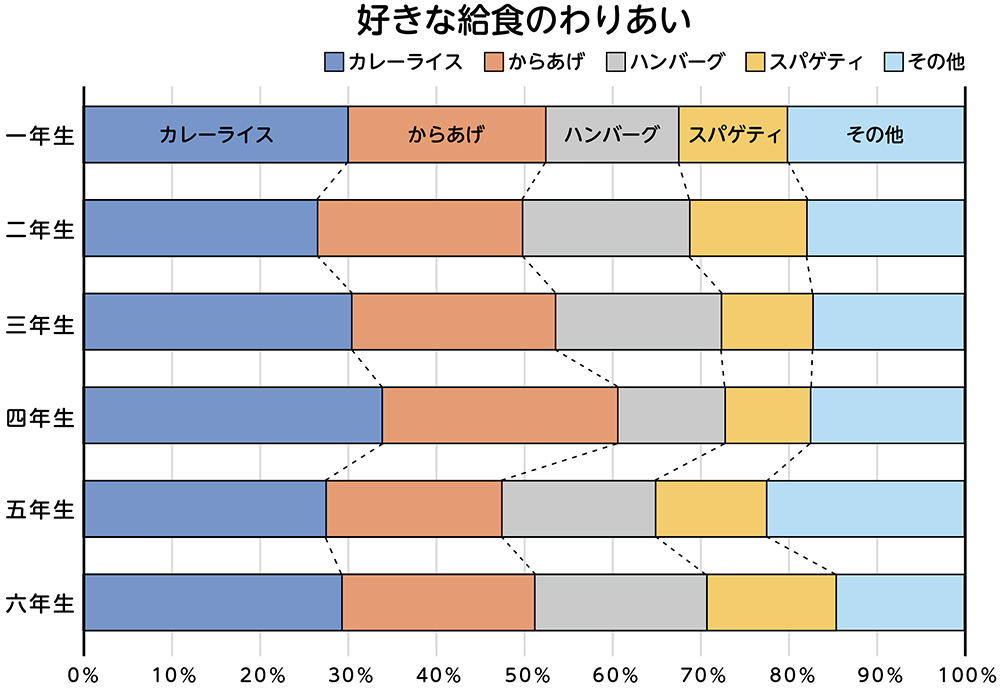
ある小学校で調べた好きな給食の学年ごとの帯グラフです。この帯グラフから、どんなことが分かりますか。
どの学年もカレーライスとからあげが好きな人が多いです。
どの学年もカレーライスが一番人気だと思います。
※そのほか、自由に発表させる。
この小学校のはずきさんも、みんなと同じようにこのグラフを見て、次のように考えました。
※まずは問題1を個人での解決や集団での解決で考えます。時間があれば問題2を扱います。

はずきさんの考えは正しいと言えるでしょうか。
〈はずきさんの考え〉
カレーライスが好きな人数が一番多いのは四年生です。からあげが好きな人も四年生が一番多いです。
はずきさんの考えは正しいと言えますか。
正しいと思います。
学年ごとの人数が分からないから、四年生が一番多いとは限らないと思います。
帯グラフは割合をグラフにしています。だから、割合が一番多いことは分かります。
四年生のカレーライスが好きな人数を求めるためには、四年生の人数が必要です。
ほかの学年の人数も知りたいです。
それでは、学年ごとの人数ともう一つグラフを見せます。
※次の表とグラフを提示する。また、これまで提示した表、棒グラフ、帯グラフを子供に配付する。
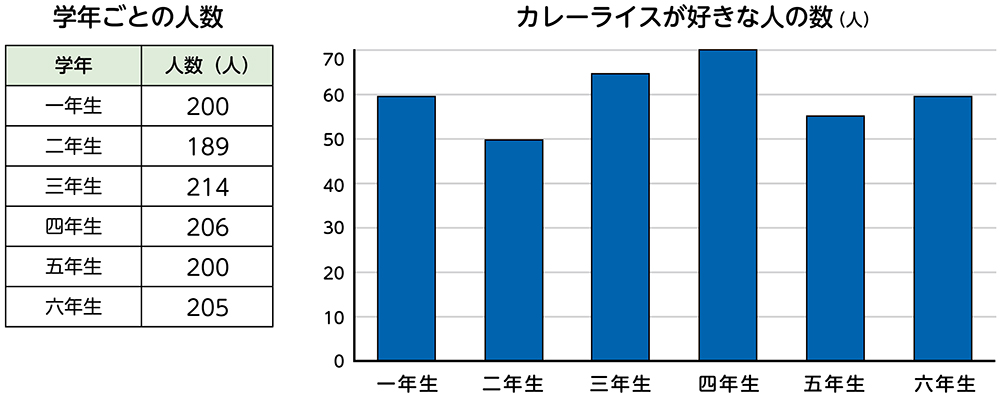
これらのデータを使えば、はずきさんの考えが正しいかどうか分かりますか。
分かりそうです。

三つの表やグラフを関係付けて、はずきさんの考えが正しいと言えるか判断しよう。
見通し
学年の人数を基に割合を比べると分かる。
自力解決の様子
A つまずいている子
どのグラフや表に目を付ければよいか分からない。
B 素朴に解いている子
棒グラフからカレーライスが好きな人数について、四年生が一番多いことは読み取れるが、からあげについては、帯グラフと表を使って人数を求めることができない。
C ねらい通り解いている子
からあげについても、帯グラフと表とを使って人数を求めて、どの学年が一番多いか判断することができている。
学び合いの計画
Aの子供については、次のBの子供と同様の指導に先立ち、表の数値だけでは各学年のカレーライスが好きな人数が分からないことを確認します。
イラスト/横井智美

