小5算数「四角形と三角形の面積」指導アイデア《台形の面積の求め方》

執筆/神奈川県横浜市立さつきが丘小学校教諭・岡田かおり
監修/東京都国立教育政策研究所教育課程調査官・加固希支男、神奈川県横浜市立伊勢山小学校副校長・黒木正人
目次
年間指導計画
・整数と小数
・体積
・合同な図形
・比例
・小数のかけ算
・平均
・単位量あたりの大きさ
・小数のわり算
・速さ
・図形の角
・整数の性質
・分数のたし算とひき算
・わり算と分数
・面積
・割合
・帯グラフと円グラフ
・円と正多角形
・□と△を使った式
単元の展開(各時の主な学習活動内容)
第1時 平行四辺形の面積の求め方を考え、説明することができる。
第2時 平行四辺形の面積の公式をつくり出し、それを適用して面積を求めることができる。
第3時 高さが平行四辺形の外にある場合でも、平行四辺形の面積の公式を適用できることを理解する。
第4時 三角形の面積の求め方を考え、説明することができる。
第5時 三角形の面積の公式をつくり出し、それを適用して面積を求めることができる。
第6時 高さが三角形の外にある場合でも、平行四辺形の面積の公式を適用できることを理解する。
第7時(本時)台形の面積の求め方を考え、説明することができる。
第8時 台形の面積の公式をつくり出し、それを適用して面積を求めることができる。
第9時 ひし形の面積の求め方を考え、説明することができる。また、ひし形の面積の公式をつくり出し、それを適用して面積を求めることができる。
第10時 学習内容の習熟・定着を図る。
本時のねらい
台形の性質に着目し、面積の求め方を考え、説明することができる。
評価規準
- 台形の性質に着目し、台形の面積の求め方を既習の求積方法に帰着して考え、筋道立てて説明する。
本時の教材のポイント
台形の面積の公式をただ覚えるのではなく、これまで学んだ図形の面積の求め方を基に、台形の面積の求め方を自ら考え、公式を導き出していくことを大切にしています。平行四辺形や三角形の面積の考え方を生かせば、台形の面積も自分の力で求められることに気付くようにしていきます。これまでの学びを活用して新しい図形でも見通しをもって取り組める子供を育成することも大切です。
本時では、「台形も、これまでの図形と同じように面積の求め方を考えられないかな?」という問いを基に学び進めます。子供たちは、対角線を引いて2つの三角形に分けたり、合同な台形を組み合わせて平行四辺形にしたりと、これまでの学びを使って台形を見つめ直していきます。それぞれの考えを表した式を比べながら、「図形をどのように見たのか」「もっと式を簡単に表せないのか」を考える中で、台形の面積求め方の共通する考え方に気付きます。そして、どこに着目すれば台形の面積を求められるのかをふり返ることで、公式へと導いていけるようにしていきます。
本時の展開
これまで、平行四辺形と三角形の面積の求め方を考えてきましたね。どのように考えたら求めることができましたか。
求められる形に変えたらできました。
例えば、長方形や平行四辺形に形を変えました。
いつでも使える公式もできました。
図形のどこに注目したら、公式はできましたか。
底辺と高さに注目しました。
そうすると1つ分の大きさが決まって、かけ算で求められました。
次はどんな形の面積が求められそうですか。
前の時間のふり返りに、平行四辺形や三角形と同じように考えたら、台形の面積も求められるのかなと書きました。
同じように、求められる面積の形が見えたら、求められそうです。
台形は、上と下の辺の長さが違うけれどできるのかな。
それでは、平行四辺形や三角形と同じように、求められる面積の形が見えたら台形の面積を求められるか考えてみましょう。
※求める台形を提示する。
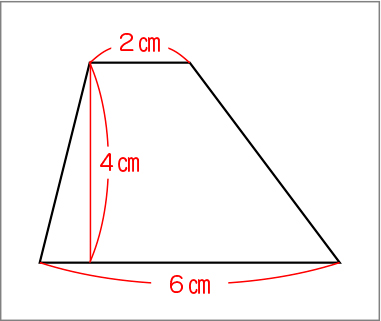

台形も、面積が求められる図形を見付けて、面積の求め方を考えよう。
見通し
台形の真ん中を切ったら、平行四辺形になりそうだ。
台形も四角形だから対角線を引いたら三角形が見えるよ。
三角形のときのように、台形をもう1つ付けたら平行四辺形になるかも。
自力解決の様子
A つまずいている子
・切ったり移動したりして求められる形にできるが、その後、止まってしまっている。
B 素朴に解いている子
・三角形2つと、長方形に分けて考えている。
C ねらい通り解いている子
・台形を半分に切り、平行四辺形にして求めている。
・合同な台形を2つ合わせ、平行四辺形にして求めている。
・台形に対角線を引いて三角形2つにして求め、式をまとめようとしている。
全体発表とそれぞれの考えの関連付け
それではどのように求めましたか。
C1 このように、三角形2つと長方形に分けました。
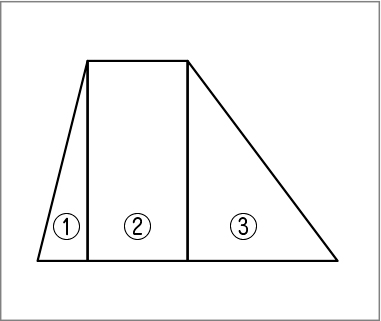
C1 それぞれ分けた図形の面積を求めると、①1×4÷2=2、②4×2=8、③3×4÷2=6。全部を合わせて、2+8+6=16。答えは16㎠です。
たくさん分けて考える方法もあったのですね。
だけど、計算が多くて大変になると思います。
このように、合同な台形をひっくり返して、くっつけると平行四辺形になりました。
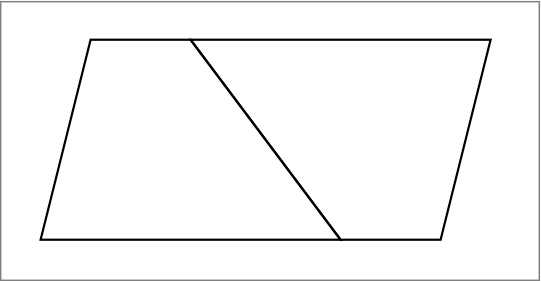
C2 同じように考えて計算しました。底辺が6㎝で、上の辺が2㎝なので、平行四辺形の底辺が、6+2で8㎝になります。高さは4㎝なので、8×4=32です。台形1つだけを求めればいいので、32÷2=16と考えました。式に表すと8×4÷2=16。答えは16㎠です。
C3 私も同じように平行四辺形にしましたが、違う求め方で考えました。このように、台形を半分に切って、切った台形をひっくり返して付けました。
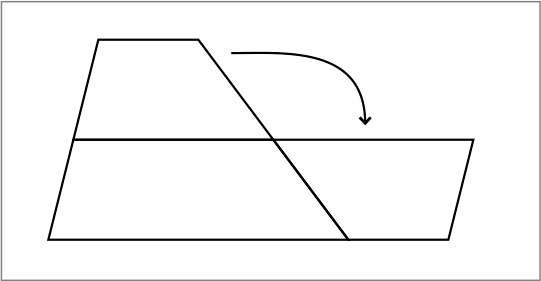
同じ平行四辺形だけど、さっきより小さい平行四辺形ですね。
C3 高さが半分になっているからですね。
式はどうなるのかな。
C3 さっきと同じように、底辺は6+2で8㎝、高さは半分になったので4÷2です。つまり、8×4÷2=16。答えは16㎠です。
さっきと同じ式ですね。
C4 私は三角形にして考えました。台形に対角線を引くと、三角形が2つできます。
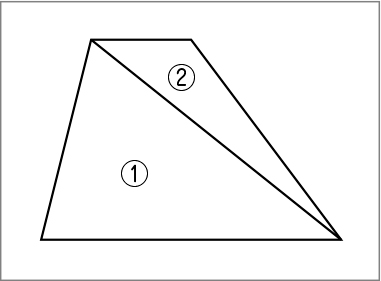
C4 できた三角形を①②とすると、①の三角形は、底辺が6㎝高さが4㎝なので、6×4÷2=12。②の三角形は、底辺が2㎝高さが4㎝なので、2×4÷2=4。2つの三角形を合わせて、12+4=16。答えは16㎠です。
同じように反対側の対角線でも、三角形2つにする考え方はできます。
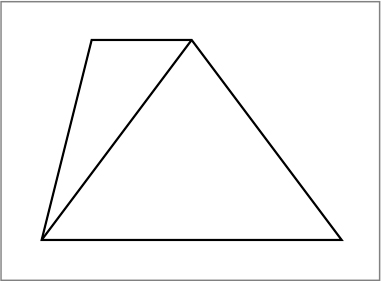
いろいろな方法がありますね。
みんなだったらどの考えを使いますか。
三角形2つの方法を使います。計算が少ないからです。
数字をそのまま使えるからいいと思います。
数字をそのまま使えるとはどういうことですか。
台形の、下の辺と上の辺と高さを使えば求められるからです。
たくさん分ける考えだと、計算が増えるので、できるだけ少ない計算だといいと思います。
なるほど。台形の上の辺と下の辺という言葉が出てきましたが、実は名前があって、上の辺を上底、下の辺を下底と言います。
新しい名前ですね。そう考えると、平行四辺形の考えも、上底と下底と高さを使っていると思います。
ということは台形の面積は、上底と下底と高さがポイントなのかもしれないです。
では、次回はそこに着目して公式にできるか考えてみましょう。
まとめ
- 台形の面積も、面積が求められる図形に変えれば求められる。
- 台形の面積でポイントは、上底、下底、高さ。
感想例
- 台形の面積も、面積が求められる図形に変えたら、求めることができた。台形の上底と下底と高さを使って求められたから、そこがポイントだと気付けました。次回は、そこに着目して、いつでも使える公式を導き出せるようにしたいです。
ポイント&アドバイス
構成/桧貝卓哉 イラスト/横井智美 図版作成/永井俊彦

